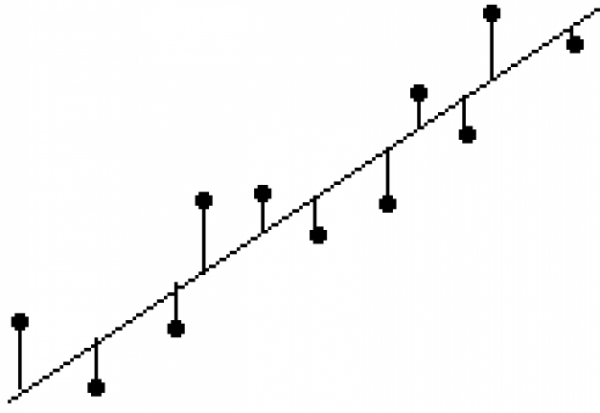
Aqui estão algumas considerações sobre por que a análise de resíduos ainda é necessária, mesmo quando se tem o valor de "S":

1.⁠ ⁠*Qualidade do Ajuste*: O erro padrão fornece uma medida geral da precisão das previsões, mas não revela informações detalhadas sobre como os dados se comportam em relação à linha de regressão. A análise de resíduos permite identificar padrões que podem indicar problemas no modelo.

2.⁠ ⁠*Assunções do Modelo*: A regressão linear faz várias suposições, como a linearidade, a homocedasticidade (variância constante dos resíduos) e a normalidade dos resíduos. A análise de resíduos é essencial para verificar se essas suposições são atendidas. O "S" não fornece essas informações.

3.⁠ ⁠*Detectar Outliers e Influência*: A análise de resíduos ajuda a identificar outliers e pontos influentes que podem distorcer a interpretação do modelo. Mesmo que o erro padrão seja aceitável, a presença de outliers pode comprometer a validade do modelo.

4.⁠ ⁠*Identificação de Não-linearidade*: A análise visual dos resíduos (por exemplo, através de gráficos de resíduos) pode mostrar se existe uma relação não linear que não é capturada pelo modelo. O erro padrão não consegue identificar esse tipo de problema.

5.⁠ ⁠*Validação de Inferências Estatísticas*: Para realizar inferências estatísticas sobre os parâmetros do modelo (como testes de hipóteses e intervalos de confiança), é importante que as suposições da regressão sejam atendidas, algo que a análise de resíduos ajuda a confirmar.

### Conclusão

Enquanto o erro padrão "S" fornece uma ideia da precisão do modelo, a análise de resíduos é crucial para validar as suposições do modelo de regressão linear e garantir que ele seja adequado para os dados. Portanto, ambos devem ser utilizados em conjunto para uma avaliação completa e robusta do modelo.