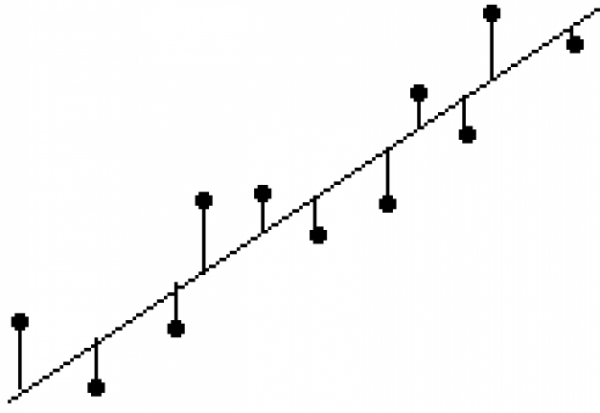
O QUE É O ERRO PADRÃO DA REGRESSÃO (S)?

O S fica menor quando os pontos de dados estão mais próximos da linha.

Na saída de regressão do software estatístico Minitab, você pode encontrar o S na seção Sumário do modelo, ao lado do R-quadrado. Ambas as estatísticas fornecem uma medida geral de quão bem o modelo se ajusta aos dados. O S é conhecido tanto como o erro padrão da regressão quanto como o erro padrão da estimativa.

O S representa a distância média em que os valores observados caem da linha de regressão. Convenientemente, ele informa como o modelo de regressão está errado usando as unidades da variável de resposta. Valores menores são melhores porque indicam que as observações estão mais próximas da linha ajustada.

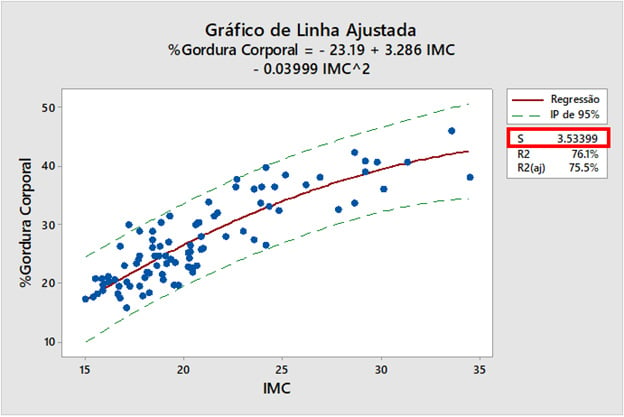
O gráfico de linha ajustada mostrado acima é do meu post, onde eu uso o IMC para prever a porcentagem de gordura corporal. O S é 3.53399, o que nos diz que a distância média dos pontos de dados da linha ajustada é de cerca de 3.5% de gordura corporal.

Ao contrário do R-quadrado, você pode usar o erro padrão da regressão para avaliar a precisão das previsões. Aproximadamente 95% das observações devem estar dentro de mais/menos 2*erro padrão da regressão em relação à linha de regressão, que é também uma aproximação para um intervalo de previsão de 95%.

Para o exemplo do IMC, cerca de 95% das observações devem estar dentro de mais/menos 7% da linha ajustada, o que é uma correspondência aproximada para o intervalo de previsão.

POR QUE EU GOSTO DO ERRO PADRÃO DA REGRESSÃO (S)

Em muitos casos, eu prefiro o erro padrão da regressão em relação ao R-quadrado. Eu amo a praticidade, a jeito intuitivo de usar as unidades naturais da variável de resposta. E, se eu precisar de previsões precisas, posso verificar rapidamente S para avaliar a precisão.

Por outro lado, o R-quadrado sem unidade não fornece uma sensação intuitiva de quão próximos os valores previstos estão em relação aos valores observados. Além disso, conforme detalhado aqui, o R-quadrado é relevante principalmente quando você precisa de previsões precisas. No entanto, você não pode usar o R-quadrado para avaliar a precisão, o que, em última análise, não ajuda.

Para ilustrar isso, vamos voltar ao exemplo do IMC. O modelo de regressão produz um R-quadrado de 76.1% e S é 3.53399% de gordura corporal. Suponha que nossa exigência seja que as previsões estejam dentro de +/- 5% do valor real.

O R-quadrado é alto o suficiente para atingir esse nível de precisão? Não tem como saber. No entanto, o S deve ser < ou = a 2.5 para produzir um intervalo de previsão suficientemente estreito de 95%. Olhando rapidamente, podemos ver que nosso modelo precisa ser mais preciso.